 Many analytics tasks and machine learning problems can be naturally expressed by iterative linear algebra programs. In the LINVIEW project, we study such complex analytical queries from the perspective of incremental processing.
Many analytics tasks and machine learning problems can be naturally expressed by iterative linear algebra programs. In the LINVIEW project, we study such complex analytical queries from the perspective of incremental processing.
Most datasets evolve through changes that are small in size compared to the overall dataset size. For example, the Internet activity of a single user, like a user’s purchase history or movie ratings, represents only a tiny portion of the collected data. Recomputing data analytics on every (moderate) dataset change is far from efficient.
We argue for incremental data analysis. The LINVIEW system implements incremental maintenance of analytical queries written as (iterative) linear algebra programs. It is a compilation framework that transforms a given program, based on matrix factorization techniques, into efficient update triggers optimized for the execution on different runtime engines. Fig. 1 gives an overview of the system.

Figure 1: The LINVIEW system overview
The current LINVIEW prototype, to be released open-source soon, supports generation of Octave programs that are optimized for the execution in multiprocessor environments, as well as Spark code for the execution on large-scale cluster platforms.
Challenges
Linear algebra operations tend to cause an avalanche effect where even very local changes to the input matrices spread out and infect all of the intermediate results and the final view, causing incremental computation to lose its performance benefit over re-evaluation. We develop techniques based on matrix factorizations to contain such epidemics of change. Our techniques make incremental view maintenance of linear algebra practical and usually substantially cheaper than re-evaluation.
For more information on the technical challenges and our contributions check out our SIGMOD14 paper.
Use Cases
LINVIEW supports incremental computation of linear algebra programs consisting of the standard matrix operations (e.g., matrix addition, multiplication, inverse, etc.). That also covers a plethora of ML algorithms including Linear regression (Ordinary Least Squares), iterative programs such as Gradient Descent, PageRank, methods for solving systems of linear equations, the power method for eigen value decomposition and many others. Currently, we are working on extending LINVIEW to deal with element-wise operations and support more ML algorithms, such as Logistic Regression, Neural Networks, and deep learning algorithms.
The LINVIEW approach is beneficial for programs that deal with expensive matrix operations, like matrix multiplication and matrix inverse. To incrementally process such programs, LINVIEW transforms those operations into computationally less expensive ones.
Performance
LINVIEW exploits the results of previous computations and low-rank of delta changes to achieve efficient incremental computation. During the compilation time, LINVIEW decides on which views to materialize, how to propagate deltas through ML programs, and how to partition the data to minimize the communication overhead. Generated incremental programs outperform their re-evaluation counterparts typically by orders of magnitude.
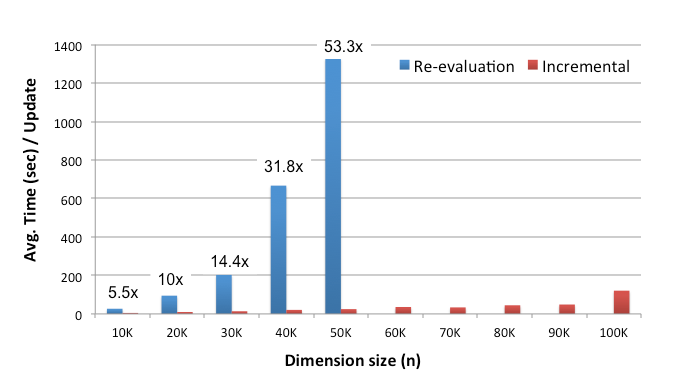
Figure 2: The LINVIEW performance for computing A16 on a 100 node Spark cluster (matrix size is n x n)
Fig. 2 compares the performance of re-evaluation and LINVIEW’s incremental strategy for computing A16, where A is a matrix of varying size. The workload consists of a stream of rank-1 updates where each update affects one row of the input matrix. On every such change, we re-evaluate or incrementally maintain the final result. The graph shows the average view refresh time for both evaluation strategies. The evaluation platform consists of a cluster with 100 Spark nodes.
The graph illustrates the superiority of incremental evaluation over re-evaluation. Notice that the LINVIEW approach has asymptotically better behavior than re-evaluation — the performance gap between these two strategies increases with higher dimensionality (re-evaluation for n > 50K exceeds one hour).
Tutorials
We plan to release LINVIEW as an open-source project soon. And more tutorials. Stay tuned…
Publications
M. Nikolic, M. El Seidy, C. Koch. “LINVIEW: Incremental View Maintenance for Complex Analytical Queries“. Proc. SIGMOD, Snowbird, Utah, 2014.
Team
Related Projects
The DBToaster project from our lab also automatically incrementalizes analytics workloads. DBToaster targets relational SQL queries, while LINVIEW focuses on (iterative) linear algebra, and the techniques employed are very different.
The Squall project from our lab is a scalable online SQL query engine built on top of Storm. Squall employs incremental techniques to achieve extremely low-latency online processing, but does not support linear algebra programs yet.
Acknowledgments
This project is supported by ERC grant 279804 ALGILE.